MATLAB によるニュートン法

平成21年度秋期基本情報技術者試験¹に出題されたニュートン法のアルゴリズムを MATLAB で作成してみた。

ニュートン法とは

ニュートン法とは，方程式の解の一つを求めるアルゴリズムである。

任意に定めた解の予測値から始めて，計算を繰り返しながらその値を真の値に近づけていく。

MATLAB によるニュートン法

ニュートン法のアルゴリズムを MATLAB で作成した。3 次方程式 3x³ – x² – 3x + 1 = 0 の解（解の予測値は 2.5）の一つを求めるアルゴリズムである。

アルゴリズムの説明

3 次方程式 a₃x³ + a₂x² + a₁x + a₀ = 0 の解の一つを，次の手順で求める。

解の予測値 x，係数 a₃，a₂，a₁，a₀ を読み込む。
3 * a₃ の値を b₂ に，2 * a₂ の値を b₁ に，1 * a₁ の値を b₀ に，それぞれ求める。
次の 1. ～ 4. の処理を一定の回数繰り返す。
1. a₃x³ + a₂x² + a₁x + a₀ の値を求め，これを f とする。
2. b₂x² + b₁x + b₀ の値を求め，これを d とする。
3. x，f，d の値を印字する。
4. x – f/d の値（解の一つにより近い値となる）を求め，これを新たな x とする。

MATLAB によるアルゴリズムの実装

以下のプログラムは，MATLAB を用いて前述のアルゴリズムを実装したものである。

a = [3, -1, -3, 1]; % 係数の定義
x = 2.5; % 解の初期値

b = zeros(1, 3); % 係数計算用の配列
b(3) = 3 * a(4); % 3次の係数
b(2) = 2 * a(3); % 2次の係数
b(1) = a(2); % 1次の係数

for n1 = 2:9
    f = ((a(4) * x + a(3)) * x + a(2)) * x + a(1);
    d = (b(3) * x + b(2)) * x + b(1);
    fprintf("%f, %f, %f\n", x, f, d);
    x = x - f / d;
end

上記のコードを実行した結果を示す。

解の一つである x = 3 が得られた。

2.500000, -2.625000, 2.750000
3.454545, 4.969947, 14.074380
3.101425, 0.874168, 9.247965
3.006900, 0.055485, 8.082941
3.000035, 0.000283, 8.000425
3.000000, 0.000000, 8.000000
3.000000, 0.000000, 8.000000
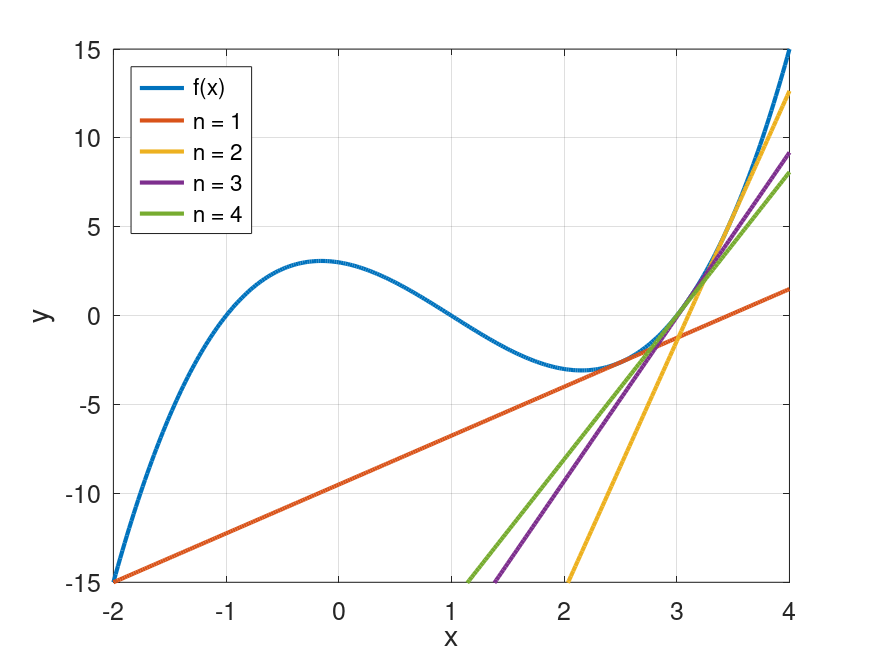
3.000000, 0.000000, 8.000000

プログラムで与えた 3 次関数の形状を確認するグラフを示す。