【MATLAB】FDTD 法で z 方向を進む 1 次元の電磁波解析

真空中の z 方向へ進む電磁波を FDTD (Finite Difference Time Domain) 法で解析する。FDTD 法で解析するコードは MATLAB で記載した。

FDTD 法は，マクスウェルの方程式におけるファラデーの方程式とアンペアの方程式を交互に用いた逐次計算による実用的な数値解析手法。日本語に訳すと「有限差分時間領域法」である。

解析の条件

z 方向は 0 ～ 2 000 mm の解析領域を設ける。z = 1 000 mm の位置に，広がり 100 mm のガウシアンパルスの電界を波源として与える。このパルスが真空中を伝搬していく様を FDTD 法でシミュレーションする。

パラメータの設定

解析に用いるパラメータを設定する。

ep=8.85418782e-12;#真空の誘電率
mu=4*pi*1e-7;#真空の透磁率
cc=1/sqrt(ep*mu);#光速
dd=2e-3;#メッシュサイズ 2 mm
NZ=1001;#z 方向の格子数
CFL=0.5;#CFL
dt=CFL*dd/cc;#時間刻み
NT=1500;#時間ステップ
zz=0:dd:dd*(NZ-1);

ee=dt/ep/dd;
hh=dt/mu/dd;
cz=(cc*dt-dd)/(cc*dt+dd);

初期条件の設定

電界，磁界の配列

z 方向へ進む電磁界として，Ex，Ey，Hz，Hy の配列を用意する。

Ex=zeros(1,NZ);
Ey=zeros(1,NZ);
Hx=zeros(1,NZ-1);
Hy=zeros(1,NZ-1);

ガウシアンパルス

電界 Ex にガウシアンパルスを与える。

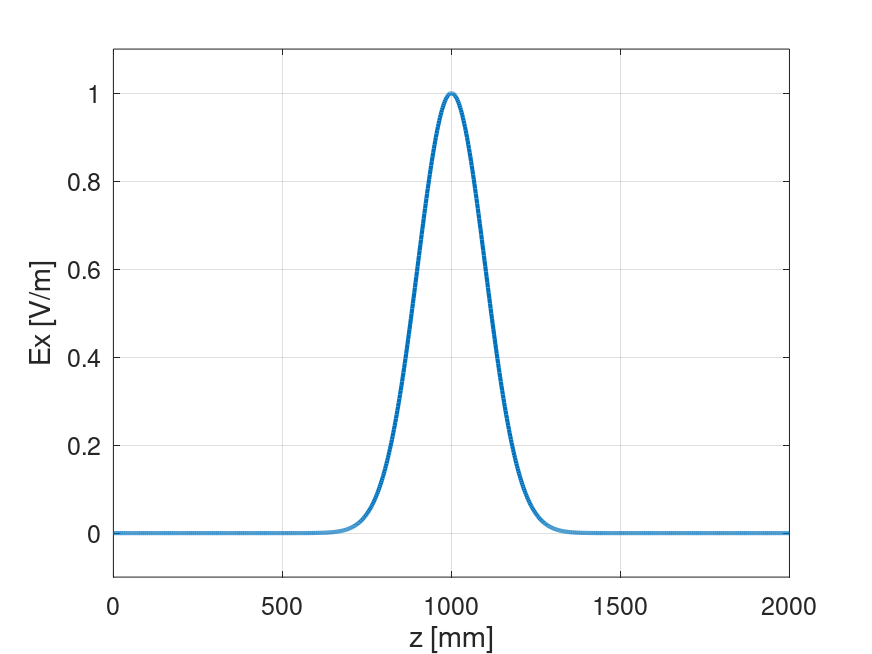
SIG=100e-3;#ガウシアンパルスの広がり
Ex=exp(-((zz-(NZ-1)/2*dd).^2)/2/SIG/SIG);

初期波源として与えたガウシアンパルスを以下に示す。

FDTD 法

FDTD 法では，電界の更新，磁界の更新を順に行う。また，解析領域の境界には，Mur の 1 次吸収境界条件を適用した。

for T=0:NT
  %===Update Ex, Ey===%
  oldEx0=Ex(1,2);
  oldExN=Ex(1,NZ-1);
  oldEy0=Ey(1,2);
  oldEyN=Ey(1,NZ-1);
  
  Ex(1,2:NZ-1)=Ex(1,2:NZ-1)-ee*(Hy(1,2:NZ-1)-Hy(1,1:NZ-2));
  Ey(1,2:NZ-1)=Ey(1,2:NZ-1)+ee*(Hx(1,2:NZ-1)-Hx(1,1:NZ-2));
  
  %===Mur's first order absorbing boundary condition===%
  Ex(1,1) =oldEx0+cz*(Ex(1,2)-Ex(1,1));
  Ey(1,1) =oldEy0+cz*(Ey(1,2)-Ey(1,1));
  
  Ex(1,NZ)=oldExN+cz*(Ex(1,NZ-1)-Ex(1,NZ));
  Ey(1,NZ)=oldEyN+cz*(Ey(1,NZ-1)-Ey(1,NZ));
  
  %===Update Hx, Hy===%
  oldHx0=Hx(1,2);
  oldHxN=Hx(1,NZ-2);
  oldHy0=Hy(1,2);
  oldHyN=Hy(1,NZ-2);
  
  Hx(1,2:NZ-2)=Hx(1,2:NZ-2)+hh*(Ey(1,3:NZ-1)-Ey(1,2:NZ-2));
  Hy(1,2:NZ-2)=Hy(1,2:NZ-2)-hh*(Ex(1,3:NZ-1)-Ex(1,2:NZ-2));
  
  %===Mur's first order absorbing boundary condition===%
  Hx(1,1) =oldHx0+cz*(Hx(1,2)-Hx(1,1));
  Hy(1,1) =oldHy0+cz*(Hy(1,2)-Hy(1,1));
  
  Hx(1,NZ-1)=oldHxN+cz*(Hx(1,NZ-2)-Hx(1,NZ-1));
  Hy(1,NZ-1)=oldHyN+cz*(Hy(1,NZ-2)-Hy(1,NZ-1));
end

まとめ

FDTD 法で z 方向を進む 1 次元の電磁波の伝搬を解析した。今回，用いた FDTD 法はシンプルなアルゴリズムであるが，正確にプログラムで記述するのに四苦八苦した。

参考文献

• 数値電磁界解析のサージ解析への適用

更新履歴

• 2024年2月15日　新規作成
• 2024年2月17日　FDTD 法のフローチャートを追加