アムダールの法則

マルチプロセッサによる並列処理において，1 プロセッサのときに対する性能向上比はアムダールの法則 (Amdahl’s Law) で説明することができる。

性能向上比 = 1 / {(1 - 並列化可能部の割合) + 並列化可能部の割合 / プロセッサ数}

並列化可能部の割合（高速化部分率）が 0.5 の場合，プロセッサ数をいくら増やしても性能向上比が 2 を超えることはない。

これは，アムダールの法則の本質である「性能向上には限界がある」ことを示している。

アムダールの法則とは

アムダールの法則とは，1967 年に米コンピュータ科学者のジーン・アムダール (Gene Amdahl) 氏によって提唱された。

IT 用語辞典 e-Words において，アムダールの法則の概要は次のように示されている（2024年11月23日調べ）。

アムダールの法則（Amdahl’s law）とは、コンピュータシステムの構成要素の一部を改良して得られる性能向上は、その要素が処理時間に寄与する度合いに制限されるという法則。並列処理の高速化の限界を示す法則として知られる。

（出典）IT 用語辞典 e-Words「アムダールの法則」

法則を提唱したアムダール氏は，1970 年代に当時の米 IBM 社のメインフレームコンピュータ製品の互換機を開発・販売していた米アムダール社 (Amdahl Corporation) の創業者としてよく知られる。

オーバヘッドの割合

問題によっては，並列化可能部の割合（高速化部分率）ではなく，オーバーヘッドの割合（1 – 高速化部分率）で与えられることがある。

例題　マルチプロセッサの性能

1 台の CPU の性能を 1 とするとき，その CPU を n 台用いたマルチプロセッサの性能 P が，

P = n / (1 + (n - 1) * a)

で表されるとする。ここで，a はオーバヘッドを表す定数である。例えば，a = 0.1，n = 4 とすると，P ≠ 3 なので，4 台の CPU から成るマルチプロセッサの性能は約 3 になる。この式で表されるマルチプロセッサの性能には限界があり，n を幾ら大きくしても P はある値以上にならない。a = 0.1 の場合，P の上限は幾らか。

解答と解説

与えられた数式の n を無限大に接近させる極限値を計算すると，次式となる。

P = 1 / a

よって，a = 0.1 の場合，n を幾ら大きくしても P は 10 以上にならない。

a = 0.1，0.2，0.4 の場合，CPU の台数 n とマルチプロセッサの性能 P との関係を下図に示す。

• a = 0.1 の場合，n を幾ら大きくしても P は 10 以上にならない。
• a = 0.2 の場合，n を幾ら大きくしても P は 5 以上にならない。
• a = 0.4 の場合，n を幾ら大きくしても P は 2.5 以上にならない。

参考　CPU の台数とマルチプロセッサの性能との関係のグラフ化

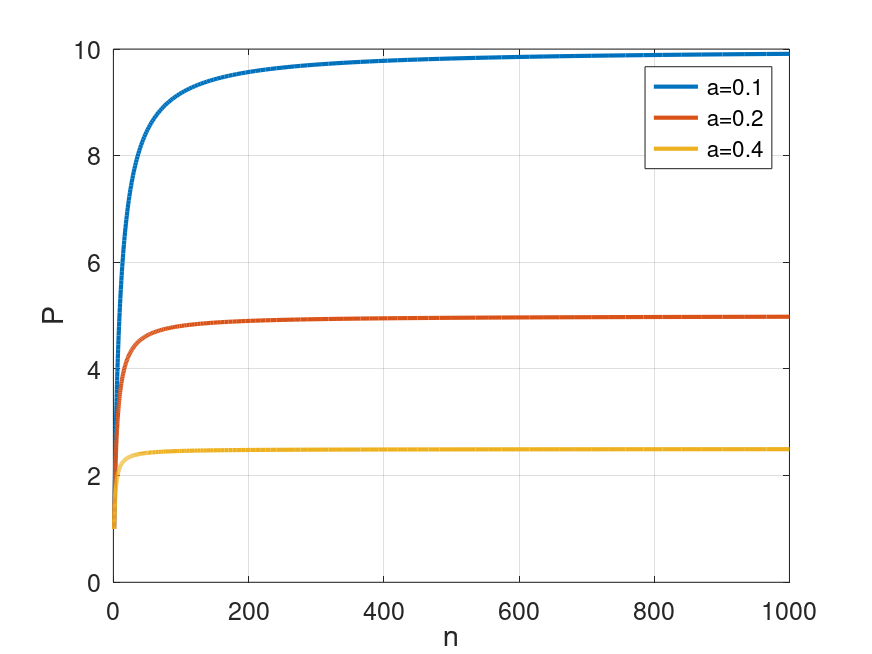
CPU の台数とマルチプロセッサの性能との関係を MATLAB / Octave でグラフ化する。

% Define the number of points and parameter values
n = logspace(0, 3, 200);
a_values = [0.1, 0.2, 0.4];

% Preallocate matrix for performance values
P = zeros(length(a_values), length(n));

% Calculate performance for each a value
for i = 1:length(a_values)
    a = a_values(i);
    P(i, :) = n ./ (1 + (n - 1) * a);
end

% Plot the results
figure(1);
plot(n, P(1, :), n, P(2, :), n, P(3, :));
xlabel('n');
ylabel('P');
grid on;
legend('a=0.1', 'a=0.2', 'a=0.4');
saveas(gcf, 'AmdalsLaw.png');

上記の MATLAB コードは，Microsoft Copilot にリファクタリングしてもらった。

更新履歴

• 2023年4月7日　新規作成
• 2023年9月8日　フォーカスキーフレーズ，メタディスクリプションを追加
• 2024年11月23日　「アムダールの法則とは」を追加